^-^
神经表面重建 - NeuS和Neuralangelo
最近更新：2025-11-07   |   字数总计：4k   |   阅读估时：14分钟   |   阅读量：次
  1. 体渲染
    1. 连续的体渲染公式
    2. 离散化的体渲染公式
    3. 基于体密度（density）的体渲染
    4. 基于有向距离函数场（SDF）的体渲染
    5. 体渲染具体实现
      1. 对物体表面的渲染
      2. 对背景的渲染
  2. 采样
    1. 无边界场景
    2. 采样距离
    3. 采样方法
  3. Neuralangelo: 多尺度从粗到细的神经表面优化
    1. 哈希网格的分辨率
    2. 数值梯度
    3. 正则项的权重
  4. 构建隐式辐射场
    1. 建立物体的SDF和RGB field
    2. 建立背景的density和RGB field

从NVIDIA的Neuralangelo这篇工作入手，梳理神经表面重建（NSR）的一些知识。

参考论文：

  • nerf
  • nerf++ / mipnerf360
  • neus
  • neuralangelo

体渲染

连续的体渲染公式

光线r=o+tv穿过的像素颜色:

采样点权重：

透过率：

不透明度：

离散化的体渲染公式

光线r=o+tv穿过的像素颜色:

$$
C(o,v)=\sum^{N}{i=1}\omega_ic_i=\sum^{N}{i=1}T_i\alpha_ic_i
$$

采样点权重：

透过率：

不透明度：

间隔长度：

基于体密度（density）的体渲染

  • 用于背景部分的渲染。

  • 体密度sigma(t)如何理解：光在t位置处碰撞到微小粒子的概率。

  • 透过率T(t)如何理解：光从光源传播到t位置处的整个过程不与微小粒子发生碰撞的概率。

  • 采样：分层采样，将光线平均划分成N个区间，每个区间随机采样一个点。

    1
    def volume_rendering_alphas_dist(densities, dists, dist_far=None):

基于有向距离函数场（SDF）的体渲染

  • 用于前景部分的渲染.

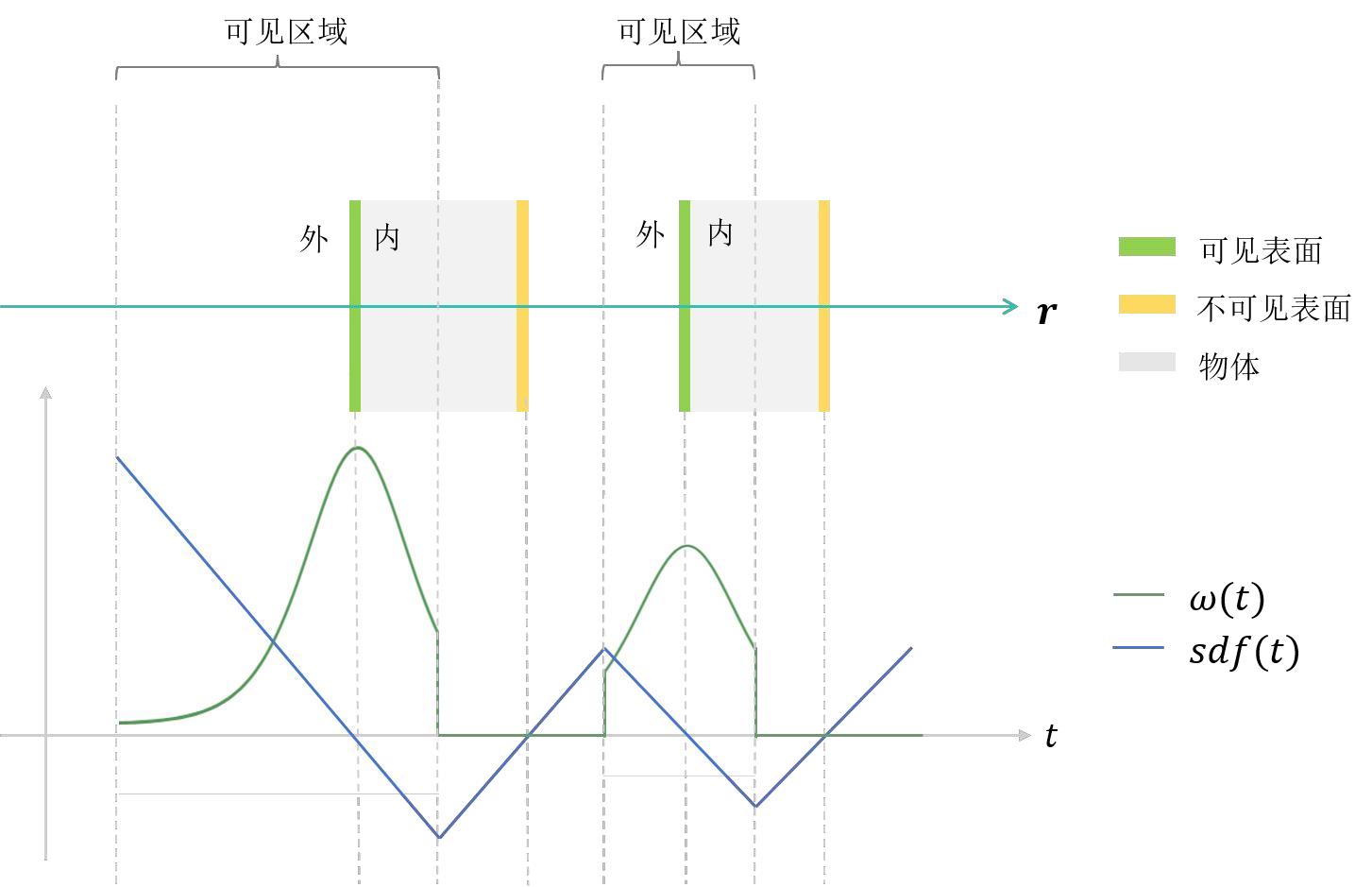
  • 与体密度场不同，SDF场的目的是提取物体表面，需要 保证光线与物体表面相交的点对于像素颜色的贡献最大 。

  • 据SDF的定义，SDF>0表示点在表面之外，SDF=0表示点在表面上，SDF<0表示点在表面之内。提取表面就需要找到SDF=0的点，那能否定义一个函数，当这个函数取得极大值时，代表此时对应的点在表面上呢？于是定义：



    • phi(x)是sigmoid函数的导数，形状呈钟形，当x=0时取得最大值，标准差为1/s.
    • 如果把SDF(P(t))作为自变量x代入phi(x)，当SDF(P(t*))=0即 P(t*)是光线和表面的交点时，phi(x)取得最大值，这保证了光线与物体表面相交的点对于像素颜色的贡献最大。因此可以将phi(x)作为采样点是否是线面交点的概率密度函数。

  • 如何计算采样点的权重：

    • 考虑无偏性，采用归一化概率密度分布的方式求出采样点的权重：

    • 上述权重公式没有顾及光线穿过不同表面的先后次序，实际上如果不同表面之间存在遮挡情况，只有先到达的表面是“可见”的，被遮挡的表面应当是“不可见的”，如果不加以限制，可能会造成颜色的混叠，与真实情况不符。所以如果存在多个SDF值为0的采样点，给予靠近相机光心的采样点更多的权重（t越小，w越大）。

    • 首先考虑SDF的计算方法：光线和表面相交于点P（t*），表面在该处向外的法向量为n，光线方向向量为v，则光线上某一点P(t)到表面的最短距离，即SDF为：

      将其代入权重公式，得到：

      又有：

      则有：

    ​ 又

    对形如

    这种积分求导的方法：

    因此：

    所以：

    ​因此：

    ​故：

    pic

体渲染具体实现

整体流程：

1
2
def render_pixels(self, pose, intr, image_size, stratified=False, sample_idx=None, ray_idx=None):
def render_rays(self, center, ray_unit, sample_idx=None, stratified=False):

  • 将采样光线与前景单位球（r=1）求交，得到在前景的near和far平面之间的采样点以及在背景部分的采样点。

    1
    def get_dist_bounds(self, center, ray_unit):

  • 分别对前景和背景进行渲染。从前景MLP和背景MLP中取出每个采样点的(1)色彩rgbs、(2)SDF或者是体密度sigma的值，进一步计算(3)透明度alphas，从采样阶段取出(4)采样间隔dists。将前景和背景采样点的这些属性拼接在一起，利用渲染公式合成每条采样光线的渲染结果。

对物体表面的渲染

1
def render_rays_object(self, center, ray_unit, near, far, outside, app, stratified=False):

  1. 在由起点center和方向ray_unit定义的光线上采样一系列点，获取这些点的t值（深度/距离）。

    1
    2
    def sample_dists_all(center, ray_unit, near, far, stratified=stratified) 
    def sample_dists_hierarchical

  2. 由p=center+tray_unit，计算每个采样点在空间中的XYZ坐标。

  3. 前传获得SDF、特征向量。

    1
    sdfs, feats = self.neural_sdf.forward(points)

  4. 计算sdf的一阶导数和二阶导数

    1
    def neural_sdf.compute_gradients(points, training=self.training, sdf=sdfs)

  5. 计算表面normal：也就是sdf归一化的一阶导数。

  6. 利用点坐标、光线方向、法向量、sdf场特征向量，前传获得RGB。

  7. 基于SDF计算不透明度。

    • 计算光线ray_unit和表面法向量normal的夹角余弦true_cos.

      注意这个夹角余弦和下面这个公式斜率的联系：

    • 下面计算sdf(t)

    1
    2
    def compute_neus_alphas(ray_unit, sdfs, gradients, dists, dist_far=far[..., None],
                                      progress=self.progress)

  8. 输出结果。

对背景的渲染

1
def render_rays_background(self, center, ray_unit, far, app_outside, stratified=False):

  1. 在由起点center和方向ray_unit定义的光线上采样一系列点，获取这些点的t值（深度/距离）。

    1
    def sample_dists_background(ray_unit, far, stratified=stratified)

    对背景光线的采样原理：

    • 一条光线与前景球体求交，可能有两个交点，按照距离view point的远近分为t_near和t_far。

    • 那么光线在前景的采样范围为【t_near，t_far】

    • 那么光线在背景的采样范围为【t_far，+∞】

    • 可以看出，背景的采样范围是无穷的，但是采样只能采有限个点。因此为了采样方便，需要将背景的采样范围限制在有限空间内。做法是将距离求倒数，使得t_far=1，无穷远处为0。具体实现是在运用下面的采样函数时，设置dist_range =（1，0）而不是（0，1）。

    1
    def sample_dists(ray_size, dist_range, intvs, stratified, device="cuda")
    • 上述映射只是为了方便采样，在采样之后需要还原采样点在光线上的t值：


  2. 由p=center+tray_unit，计算每个采样点在空间中的XYZ坐标。

    1
    def get_3D_points_from_dist(center, ray_unit, dists)

  3. 将这些采样点的空间坐标输入背景MLP中，通过前向传播，得到对应位置的rgb、体密度，然后计算不透明度。输出结果。

    1
    2
    3
    4
    5
    6
    background_nerf.forward(points, rays_unit, app_outside)
    output = dict(
                rgbs=rgbs,  # [B,R,3]
                dists=dists,  # [B,R,N,1]
                alphas=alphas,  # [B,R,N]
            )

采样

无边界场景

​ 在户外（outdoor）用相机多角度拍摄一个中心物体，其周围的背景也会被拍摄下来，而户外背景在没有遮挡的情况下可以延伸到无限远，这就导致动态深度范围很大。然而渲染只能用有限的点去做一个近似积分，因此必须把无边界场景映射到有界的空间范围内。如果相机朝向不是任意的。比如只是拍摄了前向场景（forward scene）, 此时相机平面和物方平面明显分隔于两侧，此时可以将相机的视锥体通过投影映射到NDC空间。如果相机的指向是任意的。此时相机平面和物方平面在空间中的分布就不规律了，上面的方法就不适用。此时有两种路线：

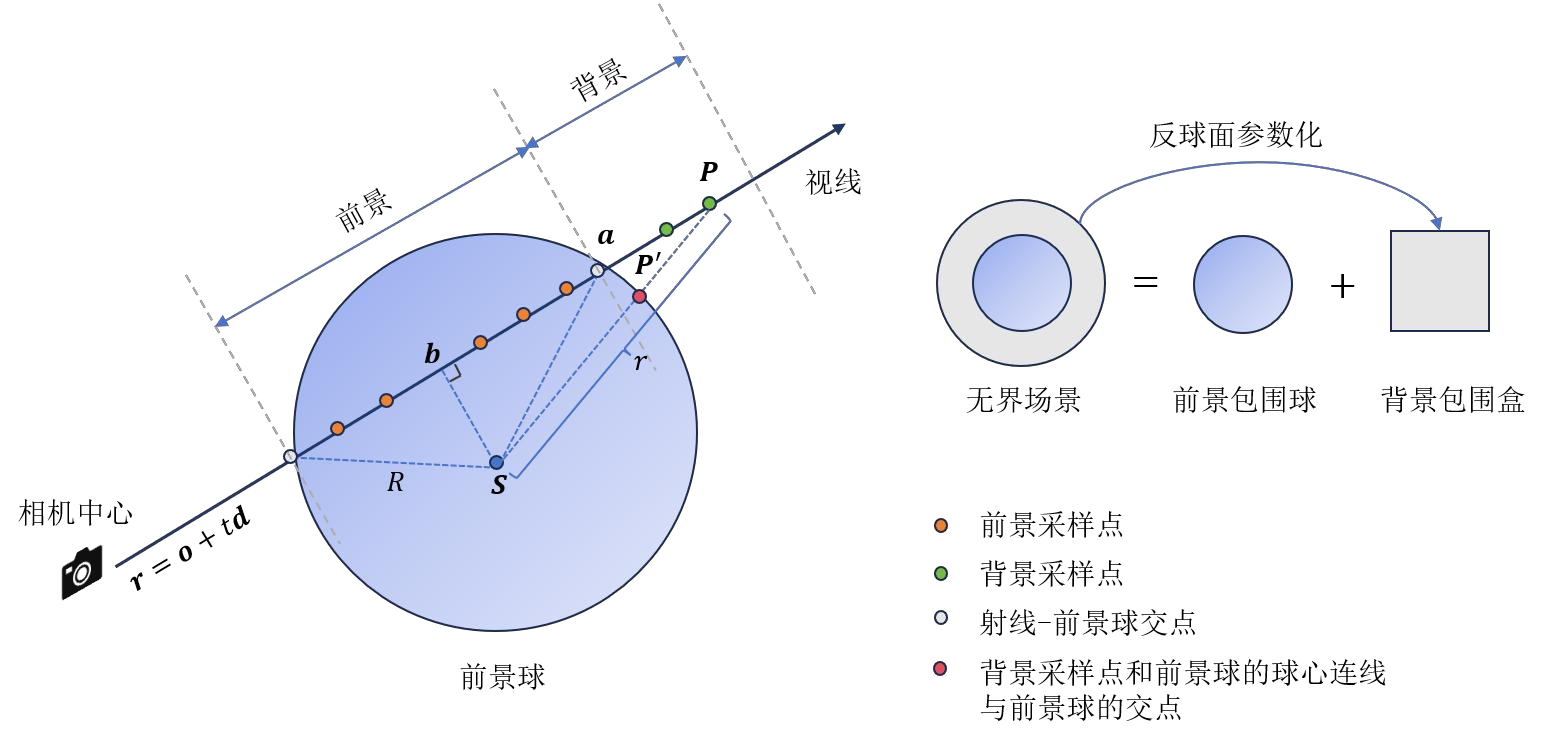
  1. NeRF++ : 把整个场景分成两部分：前景和背景。用一个半径为1的单位球框住前景，其余部分为背景。相当于有两个体素网格，球内一个、球外一个，然后分别独立地用一个MLP去估计体密度和颜色。球内的光线采样是有界的，而球外不是，因此需要对球外的部分使用反向球面参数化。
    ​ 目的是把球外坐标映射到球面上，做如下变换：

    ​ 其中

​ 给定1/r, 根据几何关系求出球外坐标映射到球面上的坐标（x’,y’,z’）：

​ 求出光线和球体的交点a

​ 作球心关于光线的垂线，垂足为b

​ 也就是说a和b都能通过上面方法求出，相当于已知数。接下来

pic
2. Mip-NeRF360 : 用一个MLP同时估计前景和背景。

采样距离

  • 视差：空间点在左右影像中的同名像点在像素坐标系的x坐标之差。

  • 深度：在相机坐标系中空间点的Z坐标。

  • 逆深度：深度的倒数。

    采样的“距离”可以是深度，也可以是视差。对于无边界场景，希望在近处的物体多被采样，在远处的物体少被采样。此时对深度进行采样不能达到这个目的，此时应当对视差（逆深度）进行等距采样。

  • 视差和深度之间的关系：

采样方法

  1. 均匀采样（Uniform sampling）: 等间距地选取采样点。最后使用线性拉伸将所有采样点的坐标限制在[near,far]之内。

  2. 分层抽样（Stratified Sampling）：将总体按某种特征或规则划分为不同的层(Strata)， 然后从每一层中随机抽取一定量的抽样单位，组成样本。具体的代码实现是：

    • 首先将整条采样光线（从near到far之间）平均分成N段，记下每段的端点的坐标（也就是r=o+td中的t值）：比如0，1，2，…

    • 然后生成N个在0-1之间符合均匀分布的随机数，代表在每一段中采样点的位置。比如0.32，0.45，0.13，…

    • 然后将二者相加，得到采样点在光线上的位置t：0.32，1.45，2.13，…

    • 最后使用线性拉伸将所有采样点的坐标限制在[near,far]之内。

    1
    2
    def sample_dists(ray_size, dist_range, intvs, stratified, device="cuda"):
        # uniform or stratified sampling

  3. 层次化采样（Hierarchical sampling）：

    （1）首先均匀采样一批coarse-points.

    （2）然后进行n次迭代，每次迭代在上一次采样基础上，增加一批fine-points.

    fine-points的选取, 可以利用coarse-points的pdf来指导，也可以设定一个值。

    1
    2
    3
    def sample_dists_all
    def sample_dists_hierarchical
    def sample_dists_from_pdf(bin, weights, intvs_fine):

与原始的NeRF同时优化粗、细两个网络不同，朗基罗遵循了NeuS的思路，只优化一个网络。具体的做法是，首先均匀采样粗采样点，然后在此基础上迭代采样精采样点，将所有采样点一起放入一个网络中。重点在于，需要根据coarse-points的SDF值来确定fine-points。粗采样点的概率weight基于具有固定标准差s-var的s密度φs（f(x)）计算的。细采样点的概率是基于一个可学习的标准差s-var的密度φs（f(x)）计算的。

Neuralangelo: 多尺度从粗到细的神经表面优化

哈希网格的分辨率

  • 为什么不从一开始就激活所有分辨率网格：

    如果一开始就激活了所有网格，那么精细的网格容易在一开始，也就是在计算SDF梯度时用到的步长比较大的时候，学到一些冗余的甚至错误的几何信息，如果后续不收敛，几何细节就难以恢复。因此，一开始只激活较粗的分辨率网格，随着迭代次数iter的增多，逐步激活更细的分辨率网格。active_levels的更新过程是三段式的，具体而言是：

    • stage 1: 计算退火层数anneal_levels。有以下几点限制：

      • 使用max[(iter - warm_up_end) // step, 1]计算。
      • 不能大于最大激活层数，不能小于初始激活层数，否则就截断为最大值或者最小值。

    • stage 2: 此后每迭代step次就多激活一层，直到达到最大层数。

    • stage 3: 保持最大激活层数直到训练结束。

  • 如何实现特定分辨率哈希网格的激活（work）：

    新建一个mask，使它的形状和哈希编码后的坐标相同。将需要激活的层对应mask上的位置赋值为1，反之则赋值为0。然后将mask和哈希编码后的坐标相乘，这样就使得激活层的编码原封不动进入后续环节，而非激活层的编码特征变为0而无法发挥作用。

1
2
def set_active_levels(self, current_iter=None)
def _get_coarse2fine_mask(self, points_enc, feat_dim)

数值梯度

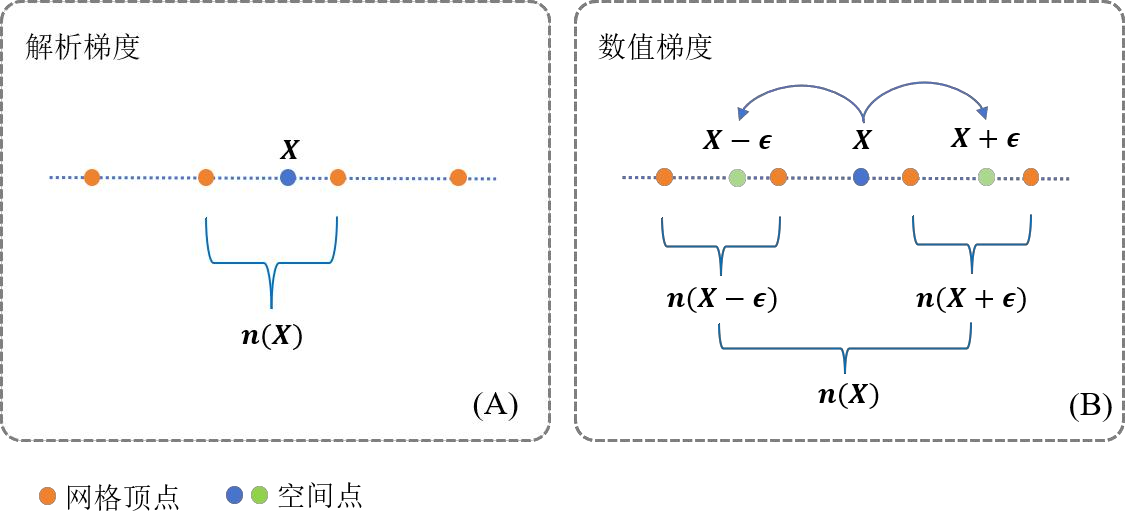
  • 数值梯度的计算 :数值梯度是解析梯度的近似，数值梯度的极限就是解析梯度，因此解析梯度的准确性更高。数值梯度虽然不够精确，但是可以通过控制步长，达到不同程度的平滑效果。一阶数值梯度（一阶差商）的计算方法为：
​ 一阶数值梯度的梯度（二阶差商）的计算方法为：

​ 实际在计算数值梯度时要从XYZ三个轴分别采样2个点，总计对邻域空间内的6个点进行采样。
pic

  • 数值梯度步长的变化 : 使用数值梯度来计算SDF的一阶和二阶导数，好处就是可以通过更改数值梯度的步长，来控制表面的平滑程度：小步长能够保留更多细节，大步长能让表面更加连续平滑。遵循“coarse to fine”的策略，计算SDF梯度时用到的步长eps是随着迭代次数iter的增多而逐渐变小的，它的更新过程：

    • 计算退火层数anneal_levels。使用max[(iter - w) // step, 1]计算。

      一般设置w = step。此时退火层数anneal_levels的是一个关于迭代次数的分段函数，在[0-3w]为1，在[3w-4w]为2，在[4w-5w]为3，… .直到迭代到最大层数。

    • 在每一次迭代过程中，从resolution的list序列中取出层数为anneal_levels的网格分辨率。

    • eps = 1/resolution[anneal_levels].

    1
    2
    def set_normal_epsilon(self)
    def compute_gradients(self, x, training=False, sdf=None)

正则项的权重

  • 迭代就是要使得loss函数值越来越小，loss包含三项：一是色彩渲染的损失、二是对SDF梯度的物理意义的限制、三是对SDF二阶导也就是物体表面的平均曲率的限制。
  • 前两点在整个从粗到细的优化过程中的重要性都保持不变，但是平均曲率限制的强度必须和计算SDF数值梯度的步长变化步调一致。所谓步调一致就是在相同时间在数值上变化相同的倍数。这样才能保证在粗网格中施加权重较大的曲率正则，能先学习到表面整体的几何形状；在细网络中施加权重较小的曲率正则，能够学习到表面的局部细节。

构建隐式辐射场

  • 隐式辐射场存储在网格或者是MLP中，并且在空间中连续可微。通过训练得到网格或者是神经网络中的一系列参数，这些参数就共同定义了这个辐射场。向辐射场中输入任一采样点的位置（p=o+td），就能够查询到该点具有的SDF、RGB属性。渲染时要查询所有采样点的相关属性，在合成像素最终的色彩时综合考虑光线上所有采样点的贡献。

建立物体的SDF和RGB field

  • SDF: 用多尺度哈希编码将采样点的空间坐标升维成特征向量，然后输入MLP。通过迭代不断更新哈希网格和MLP的参数使loss尽可能小。计算loss时使用数值梯度的方法计算SDF的一阶差商和二阶差商，SDF的值就从这个连续场取。训练后得到一个隐式存储在MLP和哈希网格中的关于坐标XYZ的SDF连续场。
  • RGB: 输入主要包含：未编码的空间坐标point_3D dim=3；用球谐函数编码后的视角view；表面向量normal dim=3；SDF网络输出的特征向量feats。训练后得到一个隐式存储在MLP中的RGB连续场。
1
2
class NeuralSDF(torch.nn.Module):
class NeuralRGB(torch.nn.Module):

建立背景的density和RGB field

  • 如果是基于NeRF++的前景、背景分离的方法，需要输入一个4维的反向球面参数化坐标、一个3维的视角方向向量。当然还要对坐标傅里叶编码、对视角球谐编码。训练后得到背景的体密度场和色彩场。
1
class BackgroundNeRF(torch.nn.Module)
2023-11-10 该篇文章被 Junfan W 打上标签: 算法

上一篇：深度学习系列 - 初学者常会遇到的问题
© RefineM (Junfan Wang)
🌊 曾记否 中流击水 浪遏飞舟 🌊 本站由Hexo驱动｜使用Hexo-theme-A4主题